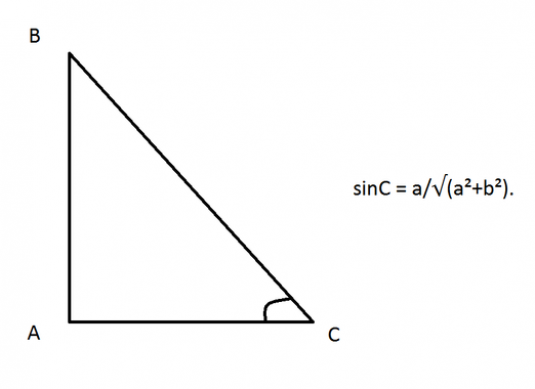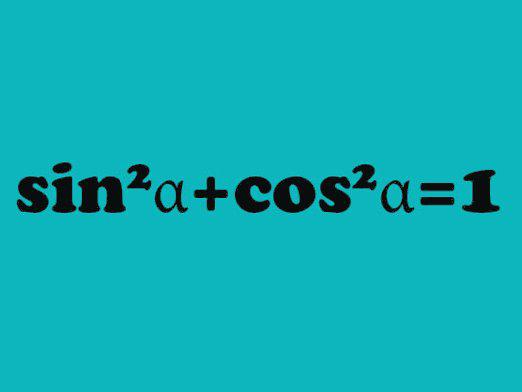How to find the sine of the outer corner?

Sine angles need to be calculated notonly in a right triangle, but in any other. To do this, it is necessary to draw the height of the triangle (perpendicular to one of the sides, lowered from the opposite corner) and solve the problem as for a right-angled triangle, using as one of the legs the height.

How to find the sine of the outer corner of a triangle

First you need to understand what an outer corner is. We have an arbitrary triangle ABC. If one of the sides, for example, AC, continues beyond the BAC angle and draws an AO beam, then the new OAB angle will be external. Here we will look for his sine.

To solve the problem, we need to drop the perpendicular BH to the side of the AU from the angle ABC. This is the height of the triangle. The course of the solution of the problem will depend on what we know.

The simplest option is if you know the angle of YOU. Then the problem is solved extremely easily. Since the ray OC is a straight line, the angle OAC = 180 °. Hence, the angle OAB and BAC are adjacent, and the sines of adjacent angles are equal in magnitude.

Let us consider another problem: in an arbitrary triangle ABC, the side is known: AB = a and the height BH = h. It is necessary to find the sine of the OAS angle. Since we now have a rectangular triangle ABN, the sine of the angle ABN will be equal to the ratio of the HH leg to the hypotenuse AB:

• sinBAH = BH / AB = h / a.

This is also easy. A more complicated problem, if the height h is known and the sides AC = c, BC = b, it is necessary to find the sine of the angle OAB.

By the Pythagorean theorem, we find the catheter of the CH of the triangle VSN:

• BC² = BH² + CH² b² = h² + CH ²,
• CH² = b² - h², CH = √ (b² - h²).

From here you can find a segment of the AS side of the AC:

• AH = AC - CH = c - √ (b² - h²).

Now we again use the Pythagorean theorem to find the third side of the AV triangle ABN:

• AB² = BH² + AH² = h² + (c - √ (b² - h²)) ².

The sine of the BAC angle is equal to the ratio of the height of the HV of the triangle to the side AB:

• sinBAC = BH / AH = h / (c - √ (b² - h²)).

Since the angles OAB and BAC are adjacent, their sines are equal in magnitude.

Thus, combining the Pythagorean theorem, the definitionsine and some other theorems (in particular, on adjacent angles), it is possible to solve almost the majority of problems on triangles, including finding the sine of the external angle. Sometimes additional constructions may be necessary: ​​to draw a height from the desired angle, to continue the side of the angle beyond its limits, and so on.