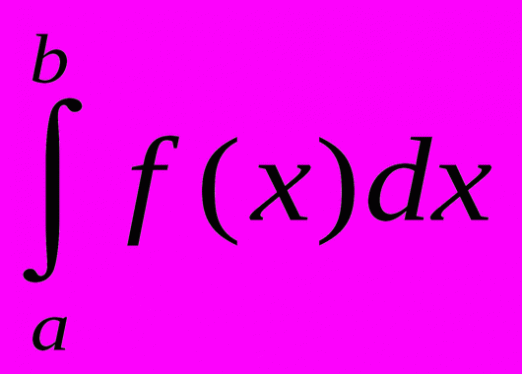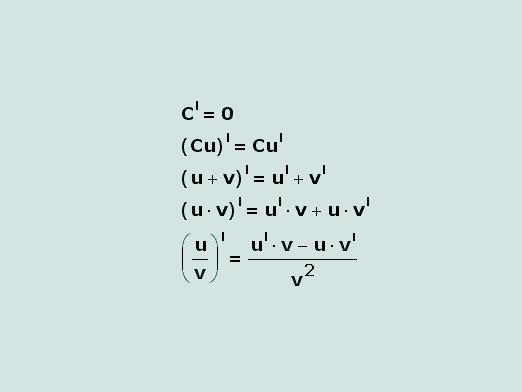How do I find a function graph?

With the task of plotting the function of the schoolchildrenencounter at the very beginning of the study of algebra and continue to build them from year to year. Starting with the graph of a linear function, for the construction of which you only need to know two points, to a parabola for which you already need 6 points, a hyperbole and a sinusoid. With each passing year the functions become more and more complicated and the construction of their graphs can not be performed on a template, it is necessary to conduct more complex studies using derivatives and limits.

Let's figure out how to find a function graph. To do this, we start with the simplest functions, the graphs of which are constructed by points, and then we will consider a plan for constructing more complex functions.

Drawing a graph of a linear function

To construct the simplest graphs use the table of values ​​of the function. The graph of a linear function is a straight line. Let's try to find the points of the graph of the function y = 4x + 5.

1. To do this, take two arbitrary values ​​of the variable x, substitute them in turn into a function, find the value of the variable y and put everything in the table.
2. We take the value x = 0 and substitute x = 0 for the function. We get: y = 4 * 0 + 5, that is, y = 5 we write this value into the table under 0. Similarly, we take x = 0, we get y = 4 * 1 + 5 , y = 9.
3. Now, in order to construct a function graph, you need to plot these points on the coordinate plane. Then you need to draw a straight line.

Construction of the graph of a quadratic function

A quadratic function is a function of the form y = ax²+ bx + c, where x is a variable, a, b, c are numbers (a is not 0). For example: y = x², y = x²+5, y = (x-3)², y = 2x²+ 3x + 5.

To construct the simplest quadratic function y = x² usually take 5-7 points. We take the values ​​for the variable x: -2, -1, 0, 1, 2 and find the values ​​of y as well as when constructing the first graph.

A graph of a quadratic function is called a parabola. After plotting the function graphs, the students have new tasks related to the schedule.

Example 1: Find the abscissa of the graph point of the function y = x², if the ordinate is 9. To solve the problem it is necessary to substitute the value 9 for the function. We obtain 9 = x² and solve this equation. x = 3 and x = -3. This can be seen on the graph of the function.

The study of the function and the construction of its graph

To construct graphs of more complex functions, several steps must be taken to study it. To do this you need:

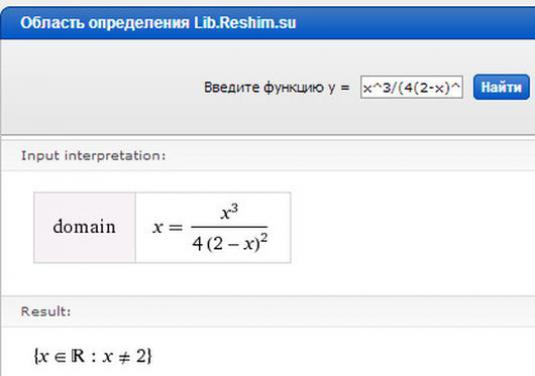
1. Find the domain of the function. A domain of definition is all values ​​that a variable x can take. From the domain of definition, it is necessary to exclude those points at which the denominator turns to 0 or the radicand becomes negative.
2. Set parity or odd function. Recall that even the function that corresponds to the condition f (-x) = f (x) is even. Its graph is symmetric with respect to Oy. The function will be odd if it corresponds to the condition f (-x) = - f (x). In this case, the graph is symmetric with respect to the origin.
3. Find the points of intersection with the coordinate axes. In order to find the abscissa of the point of intersection with the axis Ox, it is necessary to solve the equation f (x) = 0 (the ordinate in this case is equal to 0). To find the ordinate of the point of intersection with the Oy axis, it is necessary to substitute 0 for the function x (the abscissa is 0).
4. Find the asymptotes of a function. Asipotite is a straight line, to which the graph approaches infinitely, but never crosses it. Let's figure out how to find the asymptotes of the function graph.
   • The vertical asymptote is a straight line of the form x = a
   • The horizontal asymptote is a straight line of the form y = a
   • An oblique asymptote is a straight line of the form y = kx + b
5. Find the points of the extremum of the function, the intervalsincrease and decrease of the function. Let us find the extremum points of the function. To do this, it is necessary to find the first derivative and equate it to 0. It is at these points that the function can change from increasing to decreasing. We define the sign of the derivative on each interval. If the derivative is positive, then the graph of the function increases, if negative, decreases.
6. Find the points of inflection of the graph of the function, the intervals of convexity up and down.

Find the inflection points is now simple. It is only necessary to find the second derivative, then equate it to zero. Next we find the sign of the second derivative on each interval. If positive, then the graph of the function is convex down, if negative, up.