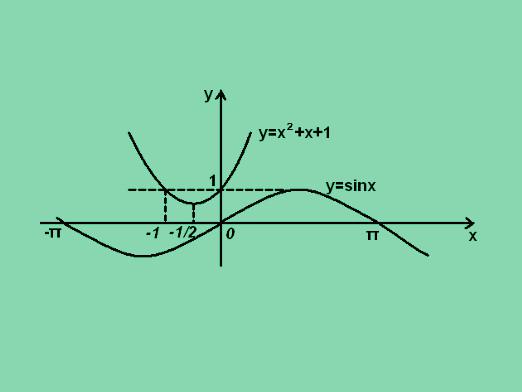
How to solve inequalities?

Not everyone knows how to solve the inequalities thattheir structure have similar and distinctive features with the equations. The equation is an exercise consisting of two parts, between which there is an equal sign, and between the parts of the inequality there may be a sign "more" or "less". Thus, before finding a solution to a specific inequality, we must understand that it is necessary to take into account the sign of a number (positive or negative) if it becomes necessary to multiply both parts by an expression. The same fact should be taken into account if it is required to square up the solution of the inequality, since squaring is carried out by multiplication.
How to solve the system of inequalities
It is much more difficult to solve systems of inequalities thanusual inequalities. How to solve the inequalities of the 9th class, we will consider with concrete examples. It should be understood that before solving square inequalities (systems) or any other system of inequalities, it is necessary to solve each inequality separately, and then to compare them. The solution of the inequality system is either a positive or a negative answer (the system has a solution or has no solution).
The task is to solve a set of inequalities:

We solve each inequality separately

We construct a numerical line on which we represent the set of solutions
Answer:

Since the collection is a union of sets of solutions, this set on the number line must be underlined by at least one line.
Solution of inequalities with a module
This example will show how to solve the inequalities with the module. So, we have a definition:
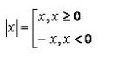
We need to solve the inequality:
| x |> 2
Before solving such an inequality, it is necessary to get rid of the module (sign)
Let's write, based on the definition:

or

Now it is necessary to solve each of the systems separately.
We construct one numerical line on which we represent sets of solutions.
As a result, we have obtained a set that unites many solutions.
Answer:

Solution of quadratic inequalities
Using the numerical straight line, consider the solution of quadratic inequalities. We have inequality:
We know that the graph of a quadratic trinomial is a parabola. We also know that the branches of a parabola are directed upwards, if a> 0.
x2-3x-4 <0
Using Viet's theorem, we find the roots x1 = - 1; x2 = 4
We draw a parabola, or rather, a sketch.
Thus, we found out that the values of the square trinomial will be less than 0 on the segment from-1 to 4.
Answer:

Many questions arise when solving doubleinequalities of the type g (x) <f (x) <q (x). Before solving double inequalities, it is necessary to decompose them into simple ones, and solve each of the simple inequalities separately. For example, expanding our example, we get as a result a system of inequalities g (x) <f (x) and f (x) <q (x), which should be solved.
In fact, there are several methods for solving inequalities, so you can use the graphical method to solve complex inequalities.
Solution of fractional inequalities
A more thorough approach requires fractionalinequality. This is due to the fact that in the process of solving certain fractional inequalities the sign may change. Before solving fractional inequalities, it is necessary to know that the interval method is used to solve them. The fractional inequality must be represented in such a way that one side of the sign looks like a fractional-rational expression, and the second - "-0". By transforming the inequality in this way, we obtain as a result f (x) / g (x)> (.
Solving inequalities by the interval method
The interval technique is based on the completeinduction, that is, to find all the possible variants for finding the solution of the inequality. This method of solution, perhaps, will not be necessary for students of the 8th grade, since they need to know how to solve the 8th class inequalities, which are the simplest exercises. But for older classes this method is irreplaceable, since it helps to solve fractional inequalities. The solution of inequalities with the help of this technique is based on the property of a continuous function, such as the preservation of the sign between the values in which it turns to 0.
We construct the graph of the polynomial. This is a continuous function that acquires a value of 0 3 times, that is, f (x) will be 0 at the points x1, x2 and x3, the roots of the polynomial. In between these points, the sign of the function is preserved.
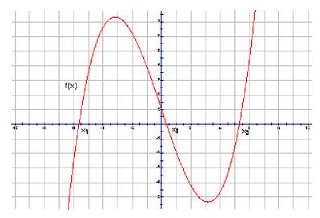
Since to solve the inequality f (x)> 0 we need a function sign, go to the coordinate line, leaving the graph.

f (x)> 0 for x (x1; x2) and for x (x3; )
f (x) x (-; x1) and for x (x2; x3)
The graph clearly shows the solutions of inequalitiesf (x) f (x)> 0 (blue for the first inequality, and red for the second). To determine To determine the sign of a function on an interval, it is sufficient that you know the sign of a function at one of the points. This technique allows us to quickly solve inequalities in which the left-hand side is factorized, because it is easy enough to find roots in such inequalities.