How to solve the biquadratic equation?

Before proceeding to the solution of the biquadratic equation, it helps to understand how it looks and how it differs from the classical quadratic equation. The equation of the form ax4 + bx2 + c = 0 is called biquadratic with onevariable (algebraic equation of the fourth degree). To bring the equation to the square form and solve through the discriminant, it is necessary to use the substitution of the variable:
- that is: x2 = t
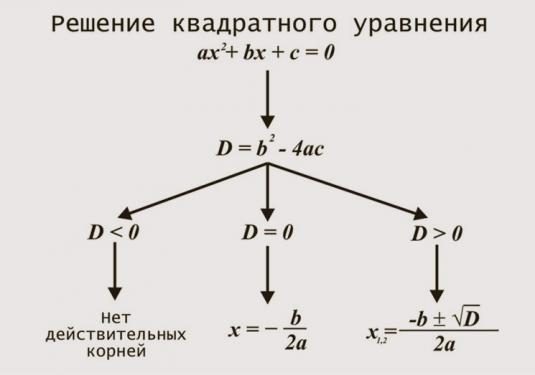
And then we have the standard equation of the form at2 + bt + c = 0
The discriminant is calculated by the formula D = b2 - 4ac.
- In the case when D = 0, the equation has one single root t1 = -b / 2a, and from this we obtain the required solution of our equation x = sqrt (t1).
- If D> 0, the equation has two roots t1 = (-b + sqrt (D)) / 2a and t2 = (-b - sqrt (D)) / 2a. Do not forget about the entered variable, and we get a finite solution x1,2 = sqrt (t1) and x3,4 = sqrt (t2)
Important note: if any of the values of ti <0, then for D = 0 the initial biquadratic solution does not have real roots, and for D> 0 there is at most one single real root.
Using the Vieta theorem
It is useful to know: in the case when we have the reduced quadratic equation (coefficient at t2 = 1), Viet's theorem is applicable, and the search for a solution is reduced to a minimum of actions:
- t1 + t2 = -b
- t1 * t2 = c
Let's consider an example:
- x4 - 3x2 + 2 = 0
using the change of variable x2 = t, we bring the quadratic equation to the form t2 - 3t; + 2 = 0.
- D = (-3)2 - 4 * 1 * 2 = 1.
The roots of the quadratic equation t1 = 2, t2 = 1.
Taking into account the introduced change of variable, we obtain the solution of the required biquadratic equation: t1 = sqrt (2); t2 = -sqrt (2); t3 = 1; t4 = -1.
To this task, we can apply Viet's theorem, since the coefficient of the variable with the highest degree is 1:
- t1 + t2 = 3
- t1 * t2 = 2
Hence t1 = 2, t2 = 1. As we see, the roots of the quadratic equation coincide in both cases, and hence the solution of the biquadratic equation will be the same.
In this paper we have considered a special case of solving a biquadratic equation, which is solved no more complicated than the classical quadratic equation.