How to find a chord?

Finding a chord in a circle, in its essence -this is a mathematical problem, and even more specifically, the problem is from the section of geometry. That is why the use of already known and proven formulas is simply necessary. In addition, you need to know the known quantities, the properties of the most different constructions in the circle and its elements, only then the required segment connecting two any points on the surface of the same circle, called a chord, will be defined.

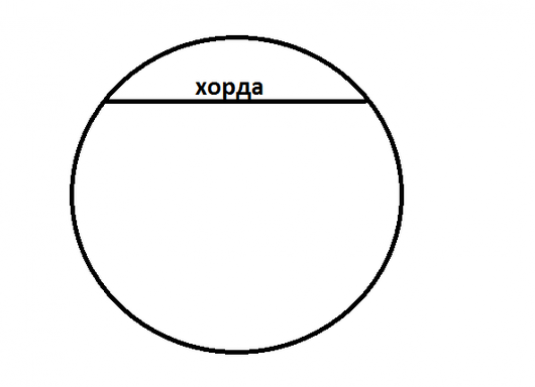
The connection of any two points on a circle by a straight line is a chord. Consequently, the longest chord of a circle is its diameter. This chord passes through the center of a given circle.

Finding a chord

To know how to find a chord, its length L,it is customary to use the formula L = 2R · sin (x / 2). If you solve this problem in an applied way, then you need a gon, ruler and protractor. With their help, the length of the tightening arc, the radius of the given circle and the angle between the radii that were drawn to the ends of the chord are determined.

To more clearly represent how to find the lengthchords, you can use an example where the center of the circle is 0, there is a chord-AB, an angle between the radii OA and OB-x, the radius of the circle R, and the angle x are known. The formed triangle ABO is isosceles because OA = OB = R. Using the formula AB = 2 * R * sin (x / 2), the chord length AB is obtained.

Another example, with other well-knownparameters, will help to understand how to find the chord of a circle. Parameters: the radius of the circle R, the length of the ASB, the smaller connecting arc, where point C is on the circle in the middle of A and B. Using the formula, the angle x in degrees is determined: x = (ACB * 180) / (pi * R). It remains only to substitute this expression in the previously obtained for the required chord length: AB = 2 * R * sin ((ACB * 90) / (pi * R)).

With these examples, one can understand that knowing the parameters of the two quantities necessary to calculate the chord length, substituting them into the formula, the third, the unknown quantity, is also determined.

The third example is when the angle is known, and alsolength of arc. The radius R is unknown. It will be equal to (ACB * 180) / (pi * x). Now the obtained expression must be substituted into the formula for determining the length of the chord: AB = ((ACB * 360) / (pi * x)) * sin (x / 2). Now you know what chord is and how to find it. This will help you in solving any mathematical and geometric problem.