How to find the length of the midline of a triangle?

You are wondering how you can calculate and find the midline of the triangle. Then for business.

Find the length of the middle line of a triangle is quite simple. Since the triangle has three sides, three corners, and possibly three middle lines.

What is a triangle:

Three sides (equilateral, isosceles)

Three corners (respectively acute, obtuse, rectangular triangles)

What is the middle line of the triangle

This is a piece. The segment connects the middle of the two sides of the triangle. Every triangle has three middle lines.

Property 1: The middle line of the triangle is parallel to the side of the triangle and is equal to its half. Therefore, to determine the midline of a triangle, it is sufficient to know the length of the third side.

Example: there is a triangle ABC, it is known that the middle side of the KN is parallel to the AC. The length of AC = 8 cm. AB = 4 cm, BC = 4 cm. Therefore, to find the midline of the triangle, it is sufficient to have AC / 2 and get the middle line of the triangle. Answer: 4 cm the middle line in the given triangle according to the existing parameters.

Property 2: If three middle lines are drawn in a triangle, then four equal similar triangles are formed. The coefficient is ½.

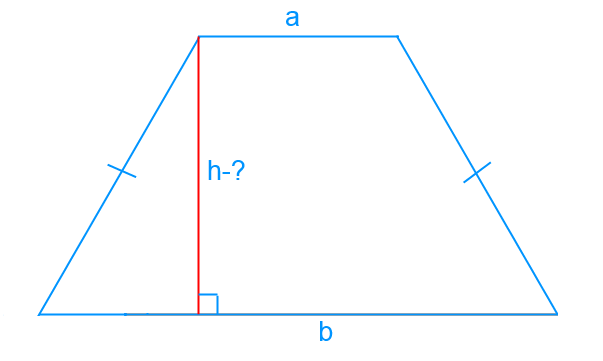
Property 3: The middle line of an equilateral triangle breaks the triangle into a trapezoid and a triangle.

An example of solving a problem: If we draw a triangle, we see that at the top of the triangle is a figure with three angles. At the bottom of the quadrilateral is a figure with two opposite sides, which are parallel to each other.

Thus, calculating the middle line of a triangle is not as difficult as it seems. Having information about the main property of the fact that the middle line is parallel to the base, we find its value.