What is a trapeze?

Every person who studied at school, in classgeometry, studied what a trapezoid. This word was used even in ancient Greece and in this language meant "a table, a table or a meal". The word "trapezium" means a quadrangular figure in which the two sides are parallel, the other two sides are not parallel at the same time.

Trapezoidal Properties

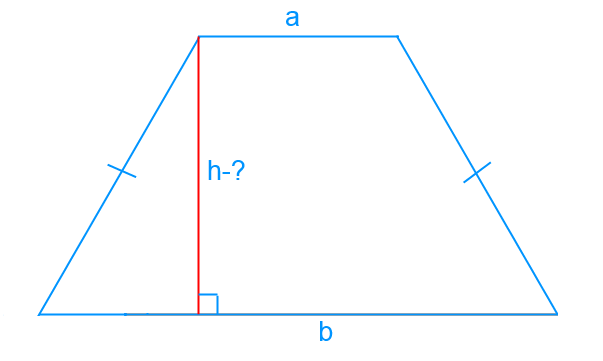
The parallel sides of the trapezoid are considered to be the basisfigures, and the other sides are lateral. Trapezium has a middle line that connects the sides in the middle. Also in this figure, you can draw a perpendicular from one point on the bottom to the other on the other base, then this perpendicular will be called the height.

There are such trapezoids:

isosceles - when the sides are the same;
rectangular - when the sides of the corners are 90 degrees.

The line of such a figure, located in the middle,is parallel to the base, is numerically equal to half the sum of the two bases. Another property concerns the angles of the trapezoid, namely, the sum of these angles is 180 degrees.

In an isosceles trapezium, the basic angles are pairwise,for example, the angle A = D, and the angle B = C. Also in the isosceles trapezium, the diagonals that connect the opposite points will be equal, we obtain AC = BD.

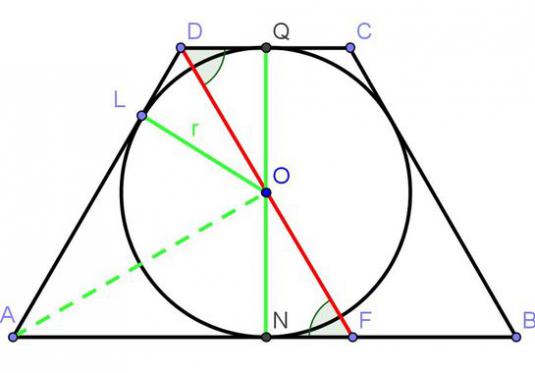
If the sum of the two main sides of the figure is fullyis identical to the sum of the lateral sides, then a circle can be inscribed into such a figure. In addition, the triangles that lie on the sides of the trapezoid are equal.

The segment that lies along the middle line andconnects the middle of the diagonals, is equal to half the difference of the sides of the base. On one line lies the point at which the lateral sides intersect and the point at which the diagonals of the trapezium join.

Area

To find out the area of the trapezoid, you must follow this formula:

S = (a + b) / 2 * h

In it: "a" and "in" - the grounds, "h" - the height of the figure.

If the lengths of the trapezoid bases are not known, andonly the height and the middle line, in this case the following formula is applicable: S = m * h. Where the value of "m" is the length of the midline. These two formulas are equivalent and we can say that the average line is m = (a + b) / 2.

To know the area of an isosceles trapezoid,you need to know the value of the angle. Here is the formula: S = (a - c * cos y) c * sin y = (b - c * cos y) c * sin y. Where a is long and b is short, c is the side, and y is the angle between the long base and the side.

See also our other articles on this site: