How to find the middle trapezoid line?

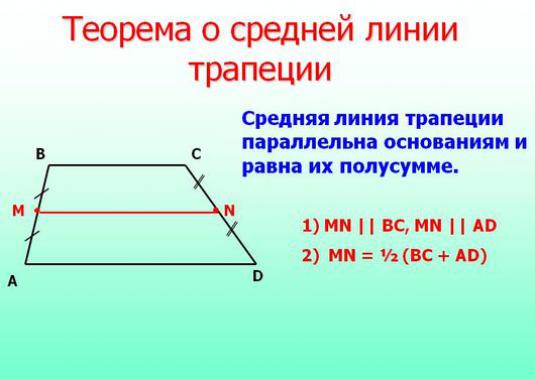
A segment of a straight line connecting the middle of the lateralsides of the trapezoid, is called the middle line of the trapezium. How to find the middle trapezium line and how it relates to other elements of this figure, we will discuss below.

The midline theorem

Draw a trapezoid in which AD is a largerbase, BC - smaller base, EF - middle line. We continue the basis AD for the point D. Draw the line BF and continue it until it intersects with the continuation of the base AD at the point O. Consider the triangles ΔBCF and ΔDFO. Angles ∟BCF = ∟DFO as vertical. CF = DF, ∟BCF = ∟FDO, because ВС // АО. Hence, the triangles ΔBCF = ΔDFO. Hence the sides BF = FO.

Now consider ΔABO and ΔEBF. ∟ABO is common for both triangles. BE / AB = ½ by condition, BF / BO = ½, since ΔBCF = ΔDFO. Consequently, the triangles ABO and EFB are similar. Hence the ratio of the sides EF / AO = ½, as well as the ratio of the other parties.

We find EF = ½ AO. It can be seen from the drawing that AO = AD + DO. DO = BC as the sides of equal triangles, hence AO = AD + BC. Hence EF = ½ AO = ½ (AD + BC). Those. The length of the middle line of the trapezoid is equal to half the sum of the bases.

Is the middle line of the trapezoid always equal to half the sum of the bases?

Suppose that there exists a special case,when EF ≠ 1 (AD + BC). Then BC ≠ DO, therefore, ΔBCF ≠ ΔDCF. But this is impossible, because they have two equal angles and sides between them. Consequently, the theorem is true under all conditions.

The midline problem

Suppose that in our trapezoid ABCD AD / BC, ∟A = 90 °, ∟C = 135 °, AB = 2 cm, the diagonal AC is perpendicular to the lateral side. Find the middle trapezoid line EF.

If ∟A = 90 °, then ∟B = 90 °, then ΔABC is rectangular.

∟BCA = ∟BCD - ∟ACD. ∟ACD = 90 ° by condition, therefore, ∟BCA = ∟BCD - ∟ACD = 135 ° - 90 ° = 45 °.

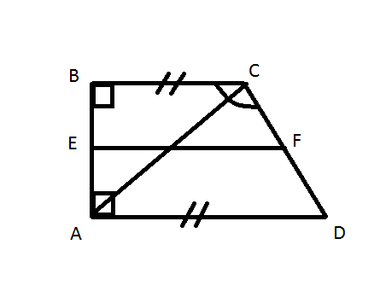
If in a rectangular triangle ΔABC one angle is 45 °, then the legs in it are equal: AB = BC = 2 cm.

Hypotenuse AC = √ (АВ² + ВС²) = √8 cm.

Consider ΔACD. ∟ACD = 90 ° by the condition. ∟CAD = ∟BCA = 45 ° as the angles formed by the secant parallel bases of the trapezium. Consequently, the legs AC = CD = √8.

Hypotenuse AD = √ (AC² + CD²) = √ (8 + 8) = √16 = 4 cm.

The average trapezium line is EF = ½ (AD + BC) = ½ (2 + 4) = 3 cm.